4 Calculus
The calculus was the first achievement of modern mathematics and it is difficult to overestimate its importance.
–Hungarian-American Mathematician John von Neumann
4.1 Intro to Numerical Calculus
In this chapter we build some of the common techniques for approximating the two primary computations in calculus: taking derivatives and evaluating definite integrals. The primary goal of this chapter is to build a solid understanding of the basic techniques for numerical differentiation and integration. These will be crucial in the later chapters of this book when we numerically integrate ordinary and partial differential equations.
Recall the typical techniques from differential calculus: the power rule, the chain rule, the product rule, the quotient rule, the differentiation rules for exponentials, inverses, and trig functions, implicit differentiation, etc. With these rules, and enough time and patience, we can find a derivative of any algebraically defined function. The truth of the matter is that not all functions are given to us algebraically, and even the ones that are given algebraically are sometimes really cumbersome.
Exercise 4.1 When a police officer fires a radar gun at a moving car it uses a laser to measure the distance from the officer to the car:
The speed of light is constant.
The time between when the laser is fired and when the light reflected off of the car is received can be measured very accurately.
Using the formula \(\text{distance} = \text{rate} \cdot \text{time}\), the time for the laser pulse to be sent and received can then be converted to a distance.
How does the radar gun then use that information to calculate the speed of the moving car?
Integration, on the other hand, is a more difficult situation. You may recall some of the techniques of integral calculus such as the power rule, \(u\)-substitution, and integration by parts. However, these tools are not enough to find an antiderviative for every given function. Furthermore, not every function can be written algebraically.
Exercise 4.2 In statistics the function known as the normal distribution (the bell curve) is defined as \[\begin{equation} N(x) = \frac{1}{\sqrt{2\pi}} e^{-x^2/2}. \end{equation}\] One of the primary computations of introductory statistics is to find the area under a portion of this curve since this area gives the probability of some event \[\begin{equation} P(a < x < b) = \int_a^b \frac{1}{\sqrt{2\pi}} e^{-x^2/2} dx. \end{equation}\] The trouble is that there is no known antiderivative of this function. Propose a method for approximating this area.
Exercise 4.3 A dam operator has control of the rate at which water is flowing out of a hydroelectric dam. He has records for the approximate flow rate through the dam over the course of a day. Propose a way for the operator to use his data to determine the total amount of water that has passed through the dam during that day.
What you have seen here are just a few examples of why you might need to use numerical calculus instead of the classical routines that you learned earlier in your mathematical career. Another typical need for numerical derivatives and integrals arises when we approximate the solutions to differential equations in the later chapters of this book.
Throughout this chapter we will make heavy use of Taylor’s Theorem to build approximations of derivatives and integrals. If you find yourself still a bit shaky on Taylor’s Theorem it would probably be wise to go back to Section 2.4 and do a quick review.
4.2 Differentiation
4.2.1 The First Derivative
Exercise 4.4 Recall from your first-semester Calculus class that the derivative of a function \(f(x)\) is defined as \[\begin{equation} f'(x) = \lim_{\Delta x \to 0} \frac{f(x+\Delta x) - f(x)}{\Delta x}. \end{equation}\] A Calculus student proposes that it would just be much easier if we dropped the limit and instead just always choose \(\Delta x\) to be some small number, like \(0.001\) or \(10^{-6}\). Discuss the following questions:
When might the Calculus student’s proposal actually work pretty well in place of calculating an actual derivative?
When might the Calculus student’s proposal fail in terms of approximating the derivative?
In this section we will build several approximation of first and second derivatives. The primary idea for each of these approximations is:
Partition the interval \([a,b]\) into \(N\) sub intervals
Define the distance between two points in the partition as \(\Delta x\).
Approximate the derivative at any point \(x\) in the interval \([a,b]\) by using linear combinations of \(f(x-\Delta x)\), \(f(x)\), \(f(x+\Delta x)\), and/or other points in the partition.
Partitioning the interval into discrete points turns the continuous problem of finding a derivative at every real point in \([a,b]\) into a discrete problem where we calculate the approximate derivative at finitely many points in \([a,b]\).
This distance \(\Delta x\) between neighbouring points in the partition is often referred to as the step size. It is also common to denote the step size by the letter \(h\). We will use both notations for the step size interchangeably, using mostly \(h\) in this section on differentiation and \(\Delta x\) in the next section on integration. Note that in general the points in the partition do not need to be equally spaced, but that is the simplest place to start. Figure 4.1 shows a depiction of the partition as well as making clear that \(h\) is the separation between each of the points in the partition.
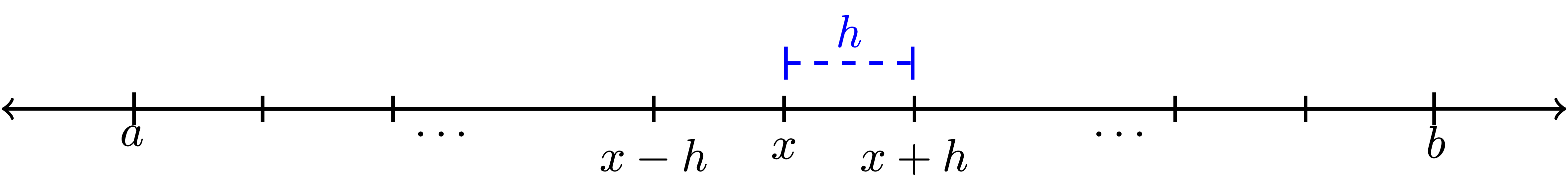
Exercise 4.5 Let us take a close look at partitions before moving on to more details about numerical differentiation.
If we partition the interval \([0,1]\) into \(3\) equal sub intervals each with length \(h\) then:
\(h = \underline{\hspace{1in}}\)
\([0,1] = [0,\underline{\hspace{0.25in}}] \cup [\underline{\hspace{0.25in}},\underline{\hspace{0.25in}}] \cup [\underline{\hspace{0.25in}},1]\)
There are four total points that define the partition. They are \(0, \underline{\hspace{0.25in}}, \underline{\hspace{0.25in}}, 1\).
If we partition the interval \([3,7]\) into \(5\) equal sub intervals each with length \(h\) then:
\(h = \underline{\hspace{1in}}\)
\([3,7] = [3,\underline{\hspace{0.25in}}] \cup [\underline{\hspace{0.25in}},\underline{\hspace{0.25in}}] \cup [\underline{\hspace{0.25in}},\underline{\hspace{0.25in}}] \cup [\underline{\hspace{0.25in}},\underline{\hspace{0.25in}}] \cup [\underline{\hspace{0.25in}},7]\)
There are 6 total points that define the partition. They are \(0, \underline{\hspace{0.25in}}, \underline{\hspace{0.25in}}, \underline{\hspace{0.25in}}, \underline{\hspace{0.25in}}, 7\).
More generally, if a closed interval \([a,b]\) contains \(N\) equal sub intervals where \[\begin{equation} [a,b] = \underbrace{[a,a+h] \cup [a+h, a+2h] \cup \cdots \cup [b-2h,b-h] \cup [b-h,b]}_{\text{$N$ total sub intervals}} \end{equation}\] then the length of each sub interval, \(h\), is given by the formula \[\begin{equation} h = \frac{\underline{\hspace{0.25in}} - \underline{\hspace{0.25in}}}{\underline{\hspace{0.25in}}}. \end{equation}\]
Exercise 4.6 In Python’s numpy library there is a nice tool called np.linspace() that partitions an interval in exactly the way that we want. The command takes the form np.linspace(a, b, n) where the interval is \([a,b]\) and \(n\) the number of points used to create the partition. For example, np.linspace(0,1,5) will produce the list of numbers 0, 0.25, 0.5, 0.75, 1. Notice that there are 5 total points, the first point is \(a\), the last point is \(b\), and there are \(4\) total sub intervals in the partition. Hence, if we want to partition the interval \([0,1]\) into 20 equal sub intervals then we would use the command np.linspace(0,1,21) which would result in a list of numbers starting with 0, 0.05, 0.1, 0.15, etc. What command would you use to partition the interval \([5,10]\) into \(100\) equal sub intervals?
Exercise 4.7 Consider the Python command np.linspace(0,1,50).
What interval does this command partition?
How many points are going to be returned?
How many equal length subintervals will we have in the resulting partition?
What is the length of each of the subintervals in the resulting partition?
Now let us get back to the discussion of numerical differentiation. If we recall that the definition of the first derivative of a function is \[\begin{equation} \begin{aligned} \frac{df(x)}{dx} = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}. \label{eqn:derivative_definition}\end{aligned} \end{equation}\] our first approximation for the first derivative is naturally \[\begin{equation} \begin{aligned} \frac{df(x)}{dx} \approx \frac{f(x+h) - f(x)}{h}=:\Delta f(x). \label{eqn:derivative_first_approx}\end{aligned} \end{equation}\] In this approximation of the derivative we have simply removed the limit and instead approximated the derivative as the slope. It should be clear that this approximation is only good if the step size \(h\) is small. In Figure 4.2 we see a graphical depiction of what we are doing to approximate the derivative. The slope of the tangent line (\(\Delta y / \Delta x\)) is what we are after, and a way to approximate it is to calculate the slope of the secant line formed by looking \(h\) units forward from the point \(x\).
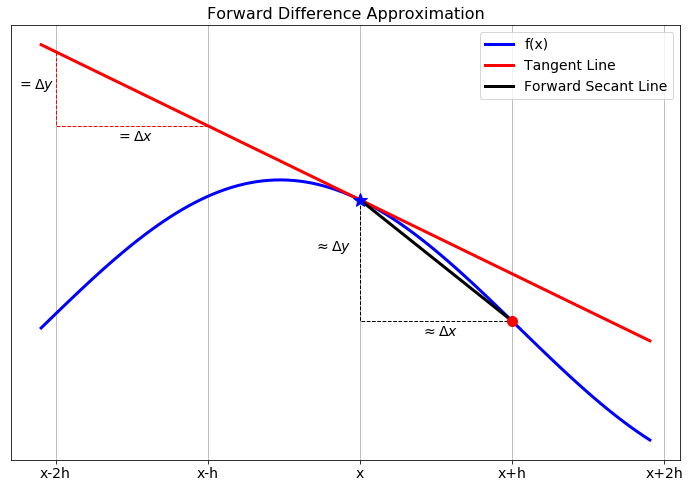
While this is the simplest and most obvious approximation for the first derivative there is a much more elegant technique, using Taylor series, for arriving at this approximation. Furthermore, the Taylor series technique gives us information about the approximation error and later will suggest an infinite family of other techniques.
4.2.2 Truncation error
Exercise 4.8 From Taylor’s Theorem we know that for an infinitely differentiable function \(f(x)\), \[\begin{equation} f(x) = f(x_0) + \frac{f'(x_0)}{1!} (x-x_0)^1 + \frac{f''(x_0)}{2!}(x-x_0)^2 + \frac{f^{(3)}(x_0)}{3!}(x-x_0)^3 + \cdots. \end{equation}\] What do we get if we replace every “\(x\)” in the Taylor Series with “\(x+h\)” and replace every “\(x_0\)” in the Taylor Series with “\(x\)?” In other words, in Figure 4.1 we want to centre the Taylor series at \(x\) and evaluate the resulting series at the point \(x+h\). \[\begin{equation} f(x+h) = \underline{\hspace{3in}} \end{equation}\]
Exercise 4.9 Solve the result from the previous exercise for \(f'(x)\) to create an approximation for \(f'(x)\) using \(f(x+h)\), \(f(x)\), and some higher order terms. (fill in the blanks and the question marks) \[\begin{equation} f'(x) = \frac{f(x+h) - ???}{??} + \underline{\hspace{2in}} \end{equation}\]
Exercise 4.10 In the formula that you developed in Exercise 4.9, if we were to truncate after the first fraction and drop everything else (called the remainder), we know that we would be introducing a truncation error into our derivative computation. If \(h\) is taken to be very small then the first term in the remainder is the largest and everything else in the remainder can be ignored (since all subsequent terms should be extremely small … pause and ponder this fact). Therefore, the amount of error we make in the derivative computation by dropping the remainder depends on the power of \(h\) in that first term in the remainder.
What is the power of \(h\) in the first term of the remainder from Exercise 4.9?
Definition 4.1 (Order of a Numerical Differentiation Scheme) The order of a numerical derivative is the power of the step size in the first term of the remainder of the rearranged Taylor Series. For example, a first order method will have “\(h^1\)” in the first term of the remainder. A second order method will have “\(h^2\)” in the first term of the remainder. Etc.
For sufficiently small step size \(h\), the error that you make by truncating the series is dominated by the first term in the remainder, which is proportional to the power of \(h\) in that term. Hence, the order of a numerical differentiation scheme tells you how the error you are making by using the approximation scheme decreases as you decrease the step-size \(h\).
Definition 4.2 (Big O Notation) We say that the error in a differentiation scheme is \(\mathcal{O}(h)\) (read: “big O of \(h\)”), if and only if there is a positive constant \(M\) such that \[\begin{equation} |\text{Error}| \le M \cdot h \end{equation}\] when \(h\) is sufficiently small. This is equivalent to saying that a differentiation method is “first order.”
More generally, we say that the error in a differentiation scheme is \(\mathcal{O}(h^k)\) (read: “big O of \(h^k\)”) if and only if there is a positive constant \(M\) such that \[\begin{equation} |\text{Error}| \leq M \cdot h^k. \end{equation}\] when \(h\) is sufficiently small. This is equivalent to saying that a differentiation scheme is “\(k^{th}\) order.”
Theorem 4.1 The approximation you derived in Exercise 4.9 gives a first order approximation of the first derivative: \[\begin{equation} f'(x) = \frac{f(x+h) - f(x)}{h} + \mathcal{O}(h). \end{equation}\] This is called the forward difference approximation of the first derivative.
Exercise 4.11 Consider the function \(f(x) = \sin(x) (1- x)\). The goal of this exercise is to make sense of the discussion of the “order” of the derivative approximation. You may want to pause first and reread the previous couple of pages.
Find \(f'(x)\) by hand.
Use your answer to part (a) to verify that \(f'(1) = -\sin(1) \approx -0.8414709848\).
To approximate the first derivative at \(x=1\) numerically with the forward-difference approximation formula from Theorem 4.1 we calculate \[\begin{equation} f'(1) \approx \frac{f(1+h) - f(1)}{h}=:\Delta f(1). \end{equation}\] We want to see how the error in the approximation behaves as \(h\) is made smaller and smaller. Fill in the table below with the derivative approximation and the absolute error associated with each given \(h\). You may want to use a spreadsheet to organize your data (be sure that you are working in radians!).
\(h\) \(\Delta f(1)\) \(|f'(1)-\Delta f(1)|\) \(2^{-1} = 0.5\) \(\frac{f(1+0.5)-f(1)}{0.5} \approx -0.99749\) \(0.15602\) \(2^{-2} = 0.25\) \(\frac{f(1+0.25)-f(1)}{0.25} \approx -0.94898\) \(0.10751\) \(2^{-3} = 0.125\) \(2^{-4}=0.0625\) \(2^{-5}\) \(2^{-6}\) \(2^{-7}\) \(2^{-8}\) \(2^{-9}\) \(2^{-10}\) There was nothing really special in part (c) about powers of 2. Use your spreadsheet to build similar tables for the following sequences of \(h\): \[\begin{equation} \begin{aligned} h &= 3^{-1}, \, 3^{-2}, \, 3^{-3}, \, \ldots \\ h &= 5^{-1}, \, 5^{-2}, \, 5^{-3}, \, \ldots \\ h &= 10^{-1}, \, 10^{-2}, \, 10^{-3}, \, \ldots \\ h &= \pi^{-1}, \, \pi^{-2}, \, \pi^{-3}, \, \ldots. \\ \end{aligned} \end{equation}\]
Observation: If you calculate a numerical derivative with a forward difference and then calculate the absolute error with a fixed value of \(h\), then what do you expect to happen to the absolute error if you divide the value of \(h\) by some positive constant \(M\)? It may be helpful at this point to go back to your table and include a column called the error reduction factor where you find the ratio of two successive absolute errors. Observe what happens to this error reduction factor as \(h\) gets smaller and smaller.
What does your answer to part (e) have to do with the approximation order of the numerical derivative method that you used?
Exercise 4.12 The following incomplete block of Python code will help to streamline the previous exercise so that you do not need to do the computation with a spreadsheet.
Comment every existing line with a thorough description.
Fill in the blanks in the code to perform the spreadsheet computations from the previous exercise.
Run the code for several different sequences of values for \(h\). Do you still observe the same result that you observed in part (e) of the previous exercise?
Run the code for several different choices of the function \(f\) and several different choices for the point \(x\). What do you observe?
import numpy as np
import matplotlib.pyplot as plt
f = lambda x: np.sin(x) * (1-x) # what does this line do?
exact = -np.sin(1) # what does this line do?
H = 2.0**(-np.arange(1,10)) # what does this line do?
AbsError = [] # start off with a blank list of errors
for h in H:
approx = # FINISH THIS LINE OF CODE
AbsError.append(np.abs((approx - exact)/exact))
if h==H[0]:
print("h=",h,"\t\t Absolute Pct Error=", AbsError[-1])
else:
err_reduction_factor = AbsError[-2]/AbsError[-1]
print("h=",h,"\t Absolute Error=", AbsError[-1],
"with error reduction",err_reduction_factor)
plt.loglog(H,AbsError,'b-*') # Why are we building a loglog plot?
plt.grid()
plt.show()Exercise 4.13 Explain the phrase: The forward difference approximation \(f'(x) \approx \frac{f(x+h)-f(x)}{h}\) is first order.
4.2.3 Efficient Coding
Now that we have a handle on how the forward-difference approximation scheme for the first derivative works and how the error depends on the step size, let us build some code that will take in a function and output the approximate first derivative on an entire interval instead of just at a single point.
Exercise 4.14 We want to build a Python function that accepts:
a mathematical function,
the bounds of an interval,
and the number of subintervals.
The function will return the forward-difference approximation of the first derivative at every point in the interval except at the right-hand side. For example, we could send the function \(f(x) = \sin(x)\), the interval \([0,2\pi]\), and tell it to split the interval into 100 subintervals. We would then get back an approximate value of the derivative \(f'(x)\) at all of the points except at \(x=2\pi\).
First of all, why can we not compute the forward-difference approximation of the derivative at the last point?
Next, fill in the blanks in the partially complete code below. Every line needs to have a comment explaining exactly what it does.
import numpy as np
import matplotlib.pyplot as plt
def ForwardDiff(f,a,b,N):
x = np.linspace(a,b,N+1) # What does this line of code do?
# What's up with the N+1 in the previous line?
h = x[1] - x[0] # What does this line of code do?
df = [] # What does this line of code do?
for j in np.arange(len(x)-1): # What does this line of code do?
# What's up with the -1 in the definition of the loop?
#
# Now we want to build the approximation
# (f(x+h) - f(x)) / h.
# Obviously "x+h" is just the next item in the list of
# x values so when we do f(x+h) mathematically we should
# write f( x[j+1] ) in Python (explain this).
# Fill in the question marks below
df.append( (f( ??? ) - f( ??? )) / h )
return df- Now we want to call upon this function to build the first order approximation of the first derivative for some function. We will use the function \(f(x) = \sin(x)\) on the interval \([0,2\pi]\) with 100 sub intervals (since we know what the answer should be). Complete the code below to call upon your
ForwardDiff()function and to plot \(f(x)\), \(f'(x)\), and the approximation of \(f'(x)\).
f = lambda x: np.sin(x)
exact_df = lambda x: np.cos(x)
a = ???
b = ???
N = 100 # What is this?
x = np.linspace(a,b,N+1)
# What does the previous line do?
# What's up with the N+1?
df = ForwardDiff(f,a,b,N) # What does this line do?
# In the next line we plot three curves:
# 1) the function f(x)
# 2) the function f'(x)
# 3) the approximation of f'(x)
# However, we do something funny with the x in the last plot. Why?
plt.plot(x,f(x),'b',x,exact_df(x),'r--',x[0:-1], df, 'k-.')
plt.grid()
plt.legend(['f(x) = sin(x)',
'exact first deriv',
'approx first deriv'])
plt.show()Implement your completed code and then test it in several ways:
Test your code on functions where you know the derivative. Be sure that you get the plots that you expect.
Test your code with a very large number of sub intervals, \(N\). What do you observe?
Test your code with small number of sub intervals, \(N\). What do you observe?
Exercise 4.15 Now let us build the first derivative function in a much smarter way – using NumPy arrays in Python. Instead of looping over all of the \(x\) values, we can take advantage of the fact that NumPy operations can act on all the elements of an array at once and hence we can do all of the function evaluations and all the subtractions and divisions at once without a loop.
The line of code
x = np.linspace(a,b,N+1)builds a numpy vector of \(N+1\) values of \(x\) starting at \(a\) and ending at \(b\). Theny = f(x)builds a vector with the function values at all the elements inx. In the following questions remember that Python indexes all lists starting at 0. Also remember that you can call on the last element of a list using an index of-1. Finally, remember that if you dox[p:q]in Python you will get a list ofxvalues starting at indexpand ending at indexq-1.What will we get if we evaluate the code
y[1:]?What will we get if we evaluate the code
y[:-1]?What will we get if we evaluate the code
y[1:] - y[:-1]?What will we get if we evaluate the code
(y[1:] - y[:-1]) / h?
Use the insight from part (1) to simplify your first order first derivative function to look like the code below.
def ForwardDiff(f,a,b,N):
x = np.linspace(a,b,N+1)
h = x[1] - x[0]
y = f(x)
df = # your line of code goes here?
return dfExercise 4.16 Write code that finds a first order approximation for the first derivative of \(f(x) = \sin(x) - x\sin(x)\) on the interval \(x \in (0,15)\). Your script should output two plots (side-by-side).
- The left-hand plot should show the function in blue and the approximate first derivative as a red dashed curve. Sample code for this exercise is given below.
import matplotlib.pyplot as plt
import numpy as np
f = lambda x: np.sin(x) - x*np.sin(x)
a = 0
b = 15
N = # make this an appropriately sized number of subintervals
x = np.linspace(a,b,N+1) # what does this line do?
y = f(x) # what does this line do?
df = ForwardDiff(f,a,b,N) # what does this line do?
fig, ax = plt.subplots(1,2) # what does this line do?
ax[0].plot(x,y,'b',x[0:-1],df,'r--') # what does this line do?
ax[0].grid()- The right-hand plot should show the absolute error between the exact derivative and the numerical derivative. You should use a logarithmic \(y\) axis for this plot.
exact = lambda x: # write a function for the exact derivative
# There is a lot going on the next line of code ... explain it.
ax[1].semilogy(x[0:-1],abs(exact(x[0:-1]) - df))
ax[1].grid()- Play with the number of sub intervals, \(N\), and demonstrate the fact that we are using a first order method to approximate the first derivative.
4.2.4 A Better First Derivative
Next we will build a more accurate numerical first derivative scheme. The derivation technique is the same: play a little algebra game with the Taylor series and see if you can get the first derivative to simplify out. This time we will be hoping to get a second order method.
Exercise 4.17 Consider again the Taylor series for an infinitely differentiable function \(f(x)\): \[\begin{equation} f(x) = f(x_0) + \frac{f'(x_0)}{1!} (x-x_0)^1 + \frac{f''(x_0)}{2!}(x-x_0)^2 + \frac{f^{(3)}(x_0)}{3!}(x-x_0)^3 + \cdots . \end{equation}\]
Replace the “\(x\)” in the Taylor Series with “\(x+h\)” and replace the “\(x_0\)” in the Taylor Series with “\(x\)” and simplify. \[\begin{equation} f(x+h) = \underline{\hspace{3in}}. \end{equation}\]
Now replace the “\(x\)” in the Taylor Series with “\(x-h\)” and replace the “\(x_0\)” in the Taylor Series with “\(x\)” and simplify. \[\begin{equation} f(x-h) = \underline{\hspace{3in}}. \end{equation}\]
Find the difference between \(f(x+h)\) and \(f(x-h)\) and simplify. Be very careful of your signs. \[\begin{equation} f(x+h) - f(x-h) = \underline{\hspace{3in}}. \end{equation}\]
Solve for \(f'(x)\) in your result from part (3). Fill in the question marks and blanks below once you have finished simplifying. \[\begin{equation} f'(x) = \frac{??? - ???}{2h} + \underline{\hspace{3in}}. \end{equation}\]
Use your result from part (4) to verify that \[\begin{equation} f'(x) = \underline{\hspace{2in}} + \mathcal{O}(h^2). \end{equation}\]
Draw a picture similar to Figure 4.2 showing what this scheme is doing graphically.
Exercise 4.18 Let us return to the function \(f(x) = \sin(x)(1- x)\) but this time we will approximate the first derivative at \(x=1\) using the formula \[\begin{equation} f'(1) \approx \frac{f(1+h) - f(1-h)}{2h}=:\delta f(1). \end{equation}\] You should already have the first derivative and the exact answer from Exercise 4.11 (if not, then go get them by hand again).
Fill in the table below with the derivative approximation and the absolute error associated with each given \(h\). You may want to use a spreadsheet to organize your data (be sure that you are working in radians!).
\(h\) \(\delta f(1)\) \(|f'(1)-\delta f(1)|\) \(2^{-1} = 0.5\) \(-0.73846\) \(0.10301\) \(2^{-2} = 0.25\) \(-0.81531\) \(0.02616\) \(2^{-3} = 0.125\) \(2^{-4}=0.0625\) \(2^{-5}\) \(2^{-6}\) \(2^{-7}\) \(2^{-8}\) \(2^{-9}\) \(2^{-10}\) There was nothing really special in part (1) about powers of 2. Use your spreadsheet to build similar tables for the following sequences of \(h\): \[\begin{equation} \begin{aligned} h &= 3^{-1}, \, 3^{-2}, \, 3^{-3}, \, \ldots \\ h &= 5^{-1}, \, 5^{-2}, \, 5^{-3}, \, \ldots \\ h &= 10^{-1}, \, 10^{-2}, \, 10^{-3}, \, \ldots \\ h &= \pi^{-1}, \, \pi^{-2}, \, \pi^{-3}, \, \ldots. \end{aligned} \end{equation}\]
Observation: If you calculate a numerical derivative with a central difference and calculate the resulting absolute error with a fixed value of \(h\), then what do you expect to happen to the absolute error if you divide the value of \(h\) by some positive constant \(M\)? It may be helpful to include a column in your table that tracks the error reduction factor as we decrease \(h\).
What does your answer to part (c) have to do with the approximation order of the numerical derivative method that you used?
Exercise 4.19 Write a Python function CentralDiff(f, a, b, N) that takes a mathematical function f, the start and end values of an interval [a, b] and the number N of subintervals to use. It should return a second order numerical approximation to the first derivative on the interval. This should be a vector with \(N-1\) entries (why?). You should try to write this code without using any loops. (Hint: This should really be a minor modification of your first order first derivative code.) Test the code on functions where you know the first derivative.
Exercise 4.20 The plot shown in Figure 4.3 shows the maximum absolute error between the exact first derivative of a function \(f(x)\) and a numerical first derivative approximation scheme. At this point we know two schemes: \[\begin{equation} f'(x) = \frac{f(x+h) - f(x)}{h} + \mathcal{O}(h) \end{equation}\] and \[\begin{equation} f'(x) = \frac{f(x+h) - f(x-h)}{2h} + \mathcal{O}(h^2). \end{equation}\]
Which curve in the plot matches with which method. How do you know?
Recreate the plot with a function of your choosing.
Code
import numpy as np
import matplotlib.pyplot as plt
# Choose a function f
f = lambda x: np.sin(x)
# Give its derivative
df = lambda x: np.cos(x)
# Choose interval
a = 0
b = 2*np.pi
m = 16 # Number of different step sizes to plot
# Pre-allocate vectors for errors
fd_error = np.zeros(m)
cd_error = np.zeros(m)
# Pre-allocate vector for step sizes
H = np.zeros(m)
# Loop over the different step sizes
for n in range(m):
N = 2**(n+2) # Number of subintervals
x = np.linspace(a, b, N+1)
y = f(x)
h = x[1]-x[0] # step size
# Calculate the derivative and approximations
exact = df(x)
forward_diff = (y[1:]-y[:-1])/h
central_diff = (y[2:]-y[:-2])/(2*h)
# save the maximum of the errors for this step size
fd_error[n] = max(abs(forward_diff - df(x[:-1])))
cd_error[n] = max(abs(central_diff - df(x[1:-1])))
H[n] = h
# Make a loglog plot of the errors agains step size
plt.loglog(H,fd_error,'b-', label='Approximation Method A')
plt.loglog(H,cd_error,'r-', label='Approximation Method B')
plt.xlabel('Steps size h')
plt.ylabel('Maximum Absolute Error')
plt.title('Comparing Two First Derivative Approximations')
plt.grid()
plt.legend()
plt.show()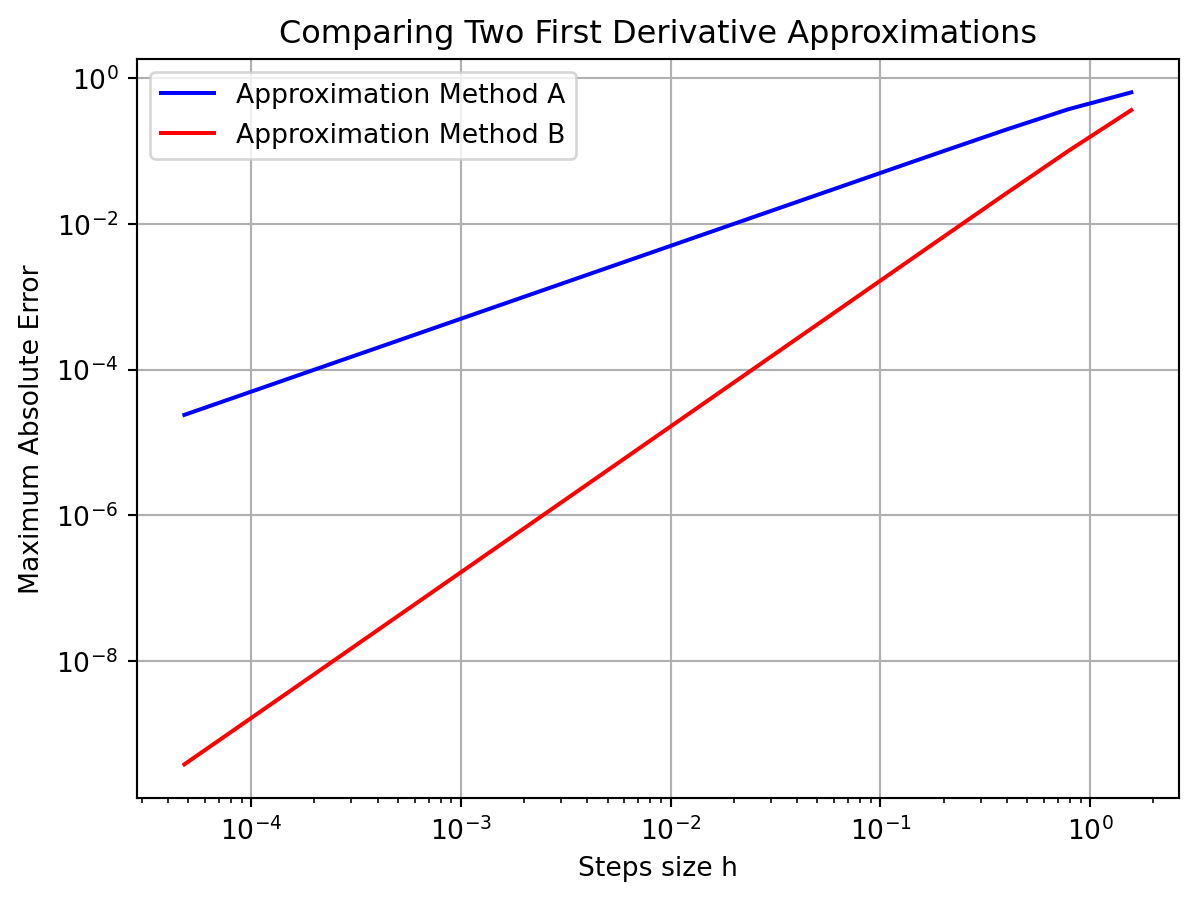
4.2.5 The Second Derivative
Now we will search for an approximation of the second derivative. Again, the game will be the same: experiment with the Taylor series and some algebra with an eye toward getting the second derivative to pop out cleanly. This time we will do the algebra in such a way that the first derivative cancels.
From the previous exercises you already have Taylor expansions of the form \(f(x+h)\) and \(f(x-h)\). Let us summarize them here since you are going to need them for future computations. \[\begin{equation} \begin{aligned} f(x+h) &= f(x) + \frac{f'(x)}{1!} h + \frac{f''(x)}{2!} h^2 + \frac{f^{(3)}(x)}{3!} h^3 + \cdots \\ f(x-h) &= f(x) - \frac{f'(x)}{1!} h + \frac{f''(x)}{2!} h^2 - \frac{f^{(3)}(x)}{3!} h^3 + \cdots. \end{aligned} \end{equation}\]
Exercise 4.21 The goal of this exercise is to use the Taylor series for \(f(x+h)\) and \(f(x-h)\) to arrive at an approximation scheme for the second derivative \(f''(x)\).
Add the Taylor series for \(f(x+h)\) and \(f(x-h)\) and combine all like terms. You should notice that several terms cancel. \[\begin{equation} f(x+h) + f(x-h) = \underline{\hspace{3in}}. \end{equation}\]
Solve your answer in part (1) for \(f''(x)\). \[\begin{equation} f''(x) = \frac{?? - 2 \cdot ?? + ??}{h^2} + \underline{\hspace{1in}}. \end{equation}\]
If we were to drop all of the terms after the fraction on the right-hand side of the previous result we would be introducing some error into the derivative computation. What does this tell us about the order of the error for the second derivative approximation scheme we just built?
Exercise 4.22 Again consider the function \(f(x) = \sin(x)(1 - x)\).
Calculate the derivative of this function and calculate the exact value of \(f''(1)\).
If we calculate the second derivative with the central difference scheme that you built in the previous exercise using \(h = 0.5\) then we get an absolute error of about 0.044466. Stop now and verify this error calculation.
Based on our previous work with the order of the error in a numerical differentiation scheme, what do you predict the error will be if we calculate \(f''(1)\) with \(h = 0.25\)? With \(h = 0.05\)? With \(h = 0.005\)? Defend your answers.
Exercise 4.23 Write a Python function SecondDiff(f, a, b, N) that takes a mathematical function f, the start and end values of an interval [a, b] and the number N of subintervals to use. It should return a second order numerical approximation to the second derivative on the interval. This should be a vector with \(N-1\) entries (why?). As before, you should write your code without using any loops.
Exercise 4.24 Test your second derivative code on the function \(f(x) = \sin(x) - x\sin(x)\) by doing the following.
Find the analytic second derivative by hand (you did this already in Exercise 4.22).
Find the numerical second derivative with the code that you just wrote.
Find the absolute difference between your numerical second derivative and the actual second derivative. This is point-by-point subtraction so you should end up with a vector of errors.
Find the maximum of your errors.
Now we want to see how the code works if you change the number of points used. Build a plot showing the value of \(h\) on the horizontal axis and the maximum error on the vertical axis. You will need to write a loop that gets the error for many different values of \(h\). Finally, it is probably best to build this plot on a log-log scale.
Discuss what you see? How do you see the fact that the numerical second derivative is second order accurate?
The table below summarizes the formulas that we have for derivatives thus far. The exercises at the end of this chapter contain several more derivative approximations. We will return to this idea when we study numerical differential equations in Chapter 6.
| Derivative | Formula | Error | Name |
|---|---|---|---|
| \(1^{st}\) | \(f'(x) \approx \frac{f(x+h) - f(x)}{h}\) | \(\mathcal{O}(h)\) | Forward Difference |
| \(1^{st}\) | \(f'(x) \approx \frac{f(x) - f(x-h)}{h}\) | \(\mathcal{O}(h)\) | Backward Difference |
| \(1^{st}\) | \(f'(x) \approx \frac{f(x+h) - f(x-h)}{2h}\) | \(\mathcal{O}(h^2)\) | Central Difference |
| \(2^{nd}\) | \(f''(x) \approx \frac{f(x+h) - 2f(x) + f(x-h)}{h^2}\) | \(\mathcal{O}(h^2)\) | Central Difference |
Exercise 4.25 Let \(f(x)\) be a twice differentiable function. We are interested in the first and second derivative of the function \(f\) at the point \(x = 1.74\). Use what you have learned in this section to answer the following questions. (For clarity, you can think of “\(f\)” as a different function in each of the following questions …it does not really matter exactly what function \(f\) is.)
Johnny used a numerical first derivative scheme with \(h = 0.1\) to approximate \(f'(1.74)\) and found an absolute error of 3.28. He then used \(h=0.01\) and found an absolute error of 0.328. What was the order of the error in his first derivative scheme? How can you tell?
Betty used a numerical first derivative scheme with \(h = 0.2\) to approximate \(f'(1.74)\) and found an absolute error of 4.32. She then used \(h=0.1\) and found an absolute error of 1.08. What numerical first derivative scheme did she likely use?
Harry wants to compute \(f''(1.74)\) to within 1% using a central difference scheme. He tries \(h=0.25\) and gets an absolute percentage error of 3.71%. What \(h\) should he try next so that his absolute percentage error is close to 1%?
4.3 Integration
Now we begin our work on the second principal computation of Calculus: evaluating a definite integral. Remember that a single-variable definite integral can be interpreted as the signed area between the curve and the \(x\) axis. In this section we will study three different techniques for approximating the value of a definite integral.
Exercise 4.26 Consider the shaded area of the region under the function plotted in Figure 4.4 between \(x=0\) and \(x=2\).
What rectangle with area 6 gives an upper bound for the area under the curve? Can you give a better upper bound?
Why must the area under the curve be greater than 3?
Is the area greater than 4? Why/Why not?
Work with your group to give an estimate of the area and provide an estimate for the amount of error that you are making.

4.3.1 Riemann Sums
In this subsection we will build our first method for approximating definite integrals. Recall from Calculus that the definition of the Riemann integral is \[\begin{equation} \begin{aligned} \int_a^b f(x) dx = \lim_{\Delta x \to 0} \sum_{j=1}^N f(x_j) \Delta x, \label{eqn:Riemann_integral}\end{aligned} \end{equation}\] where \(N\) is the number of sub intervals on the interval \([a,b]\) and \(\Delta x\) is the width of the interval. As with differentiation, we can remove the limit and have a decent approximation of the integral so long as \(N\) is large (or equivalently, as long as \(\Delta x\) is small). \[\begin{equation} \int_a^b f(x) dx \approx \sum_{j=1}^N f(x_j) \Delta x. \end{equation}\] You are likely familiar with this approximation of the integral from Calculus. The value of \(x_j\) can be chosen anywhere within the sub interval and three common choices are to use the left-aligned, the midpoint-aligned, and the right-aligned.
We see a depiction of this in Figure 4.5.
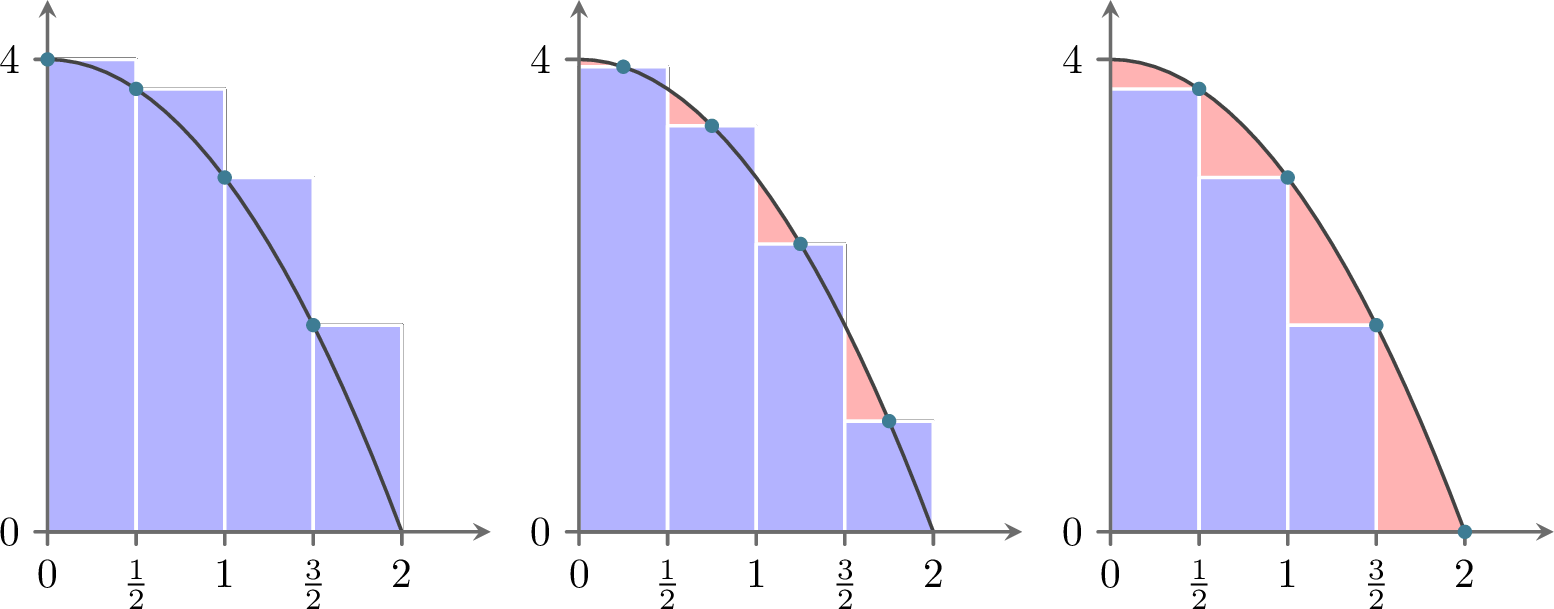
Clearly, the more rectangles we choose the closer the sum of the areas of the rectangles will get to the integral.
Exercise 4.27 Write code to approximate an integral with Riemann sums. You should ALWAYS start by writing pseudo-code as comments in your function. Your Python function should accept a Python Function, a lower bound, an upper bound, the number of subintervals, and an optional input that allows the user to designate whether they want ‘left’, ‘right’, or ‘midpoint’ rectangles. Test your code on several functions for which you know the integral. You should write your code without any loops.
Exercise 4.28 Consider the function \(f(x) = \sin(x)\). We know the antiderivative for this function, \(F(x) = -\cos(x) + C\), but in this question we are going to get a sense of the order of the error when doing Riemann Sum integration.
Find the exact value of \[\begin{equation} \int_0^{1} f(x) dx. \end{equation}\]
Now build a Riemann Sum approximation (using your code) with various values of \(\Delta x\). For all of your approximation use left-justified rectangles. Fill in the table with your results. If you want to save yourself tedious work, you will let Python create the table. You may need to recall Section 1.7 on Pandas.
| \(\Delta x\) | Approx. Integral | Absolute Error |
|---|---|---|
| \(2^{-1} = 0.5\) | ||
| \(2^{-2} = 0.25\) | ||
| \(2^{-3}\) | ||
| \(2^{-4}\) | ||
| \(2^{-5}\) | ||
| \(2^{-6}\) | ||
| \(2^{-7}\) | ||
| \(2^{-8}\) |
- There was nothing really special about powers of 2 in part (2) of this exercise. Examine other sequences of \(\Delta x\) with a goal toward answering the question:
If we find an approximation of the integral with a fixed \(\Delta x\) and find an absolute error, then what would happen to the absolute error if we divide \(\Delta x\) by some positive constant \(M\)?
Exercise 4.29 Repeat the previous exercise using right-justified rectangles.
Exercise 4.30 Create a plot with the width of the subintervals on the horizontal axis and the absolute error between your Riemann sum calculations (left, right, and midpoint) and the exact integral for a known definite integral of your choice. Your plot should be on a log-log scale. Based on your plot, what is the approximate order of the error in the Riemann sum approximation?
4.3.2 Trapezoidal Rule
Now let us turn our attention to some slightly better algorithms for calculating the value of a definite integral: The Trapezoidal Rule and Simpson’s Rule. There are many others, but in practice these two are relatively easy to implement and have reasonably good error approximations. To motivate the idea of the Trapezoid rule consider Figure 4.6. It is plain to see that trapezoids will make better approximations than rectangles at least in this particular case. Another way to think about using trapezoids, however, is to see the top side of the trapezoid as a secant line connecting two points on the curve. As \(\Delta x\) gets arbitrarily small, the secant lines become better and better approximations for tangent lines and are hence arbitrarily good approximations for the curve. For these reasons it seems like we should investigate how to systematically approximate definite integrals via trapezoids.
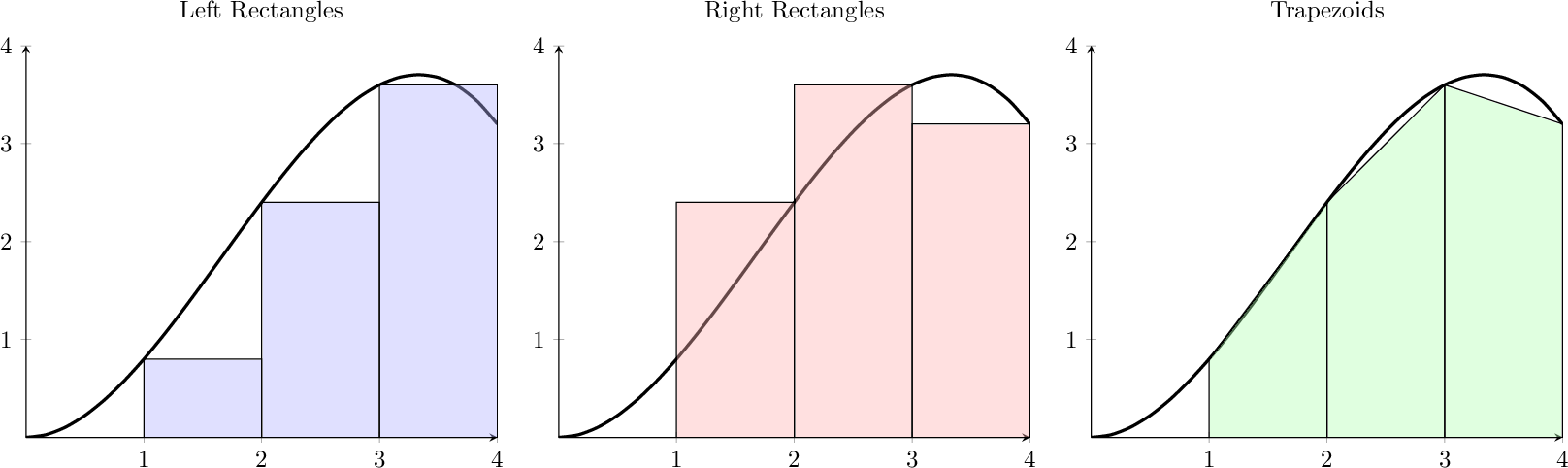
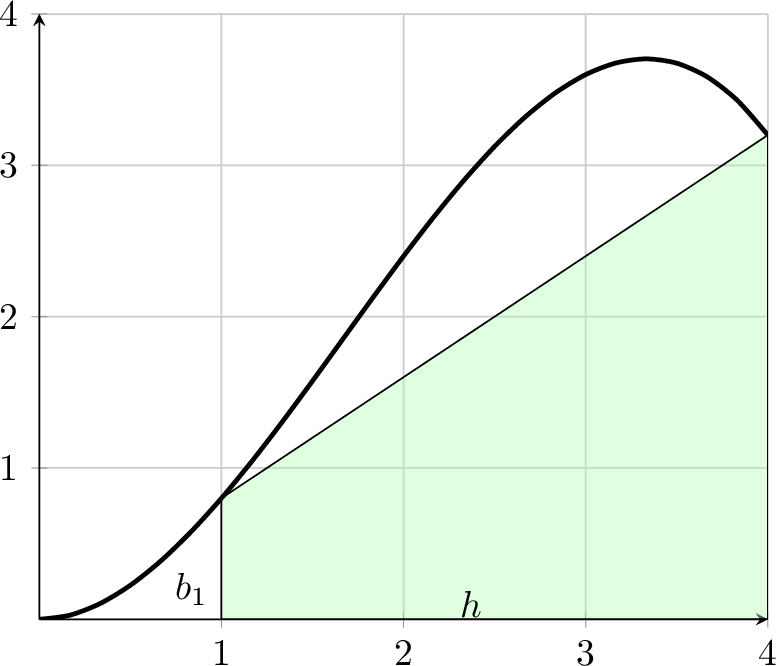
Exercise 4.31 Consider a single trapezoid approximating the area under a curve. From geometry we recall that the area of a trapezoid is \[\begin{equation} A = \frac{1}{2}\left( b_1 + b_2 \right) h, \end{equation}\] where \(b_1, b_2\) and \(h\) are marked in Figure 4.7. The function shown in the picture is \(f(x) = \frac{1}{5} x^2 (5-x)\). Find the area of the shaded region as an approximation to \[\begin{equation} \int_1^4 \left( \frac{1}{5} x^2 (5-x) \right) dx. \end{equation}\]
Now use the same idea with \(h = \Delta x = 1\) from Figure 4.6 to approximate the area under the function \(f(x) = \frac{1}{5}x^2(5-x)\) between \(x=1\) and \(x=4\) using three trapezoids.
Exercise 4.32 Again consider the function \(f(x) = \frac{1}{5}x^2(5-x)\) on the interval \([1,4]\). We want to evaluate the integral \[\begin{equation} \int_1^4 f(x) dx \end{equation}\] using trapezoids to approximate the area.
Work out the exact value of the definite integral by hand.
Summarize your answers to the previous exercises in the following table then extend the data that you have for smaller and smaller values of \(\Delta x\).
| \(\Delta x\) | Approx. Integral | Exact Integral | Abs. Error |
|---|---|---|---|
| \(3\) | |||
| \(1\) | |||
| \(1/3\) | |||
| \(1/9\) | |||
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
- From the table that you built in part (2), what do you conjecture is the order of the approximation error for the trapezoid method?
Definition 4.3 (The Trapezoidal Rule) We want to approximate \(\displaystyle \int_a^b f(x) dx\). One of the simplest ways is to approximate the area under the function with a trapezoid. Recall from basic geometry that area of a trapezoid is \(A = \frac{1}{2} (b_1 + b_2) h\). In terms of the integration problem we can do the following:
First partition \([a,b]\) into the set \(\{x_0=a, x_1, x_2, \ldots, x_{n-1},x_n=b\}\).
On each part of the partition approximate the area with a trapezoid: \[\begin{equation} A_j = \frac{1}{2} \left[ f(x_j) + f(x_{j-1}) \right]\left(x_j - x_{j-1} \right). \end{equation}\]
Approximate the integral as \[\begin{equation} \int_a^b f(x) dx = \sum_{j=1}^n A_j. \end{equation}\]
Exercise 4.33 Write code to give the trapezoidal rule approximation for the definite integral \(\int_a^b f(x) dx\). Test your code on functions where you know the definite area. Then test your code on functions where you have approximated the area by examining a plot (i.e. you have a visual estimate of the area).
Exercise 4.34 Use the code that you wrote in the previous exercise to test your conjecture about the order of the approximation error for the trapezoid rule. Integrate the function \(f(x) = \sin(x)\) from \(x=0\) to \(x=1\) with more and more trapezoids. In each case compare to the exact answer and find the absolute error. The goal is to answer the question:
If we calculate the definite integral with a fixed \(\Delta x\) and get an absolute error, \(P\), then what absolute error will we get if we use a width of \(\Delta x / M\) for some positive number \(M\)?
4.3.3 Simpsons Rule
The trapezoidal rule does a decent job approximating integrals, but ultimately you are using linear functions to approximate \(f(x)\) and the accuracy may suffer if the step size is too large or the function too non-linear. You likely notice that the trapezoidal rule will give an exact answer if you were to integrate a linear or constant function. A potentially better approach would be to get an integral that evaluates quadratic functions exactly. In order to do this we need to evaluate the function at three points (not two like the trapezoidal rule). Let us integrate a function \(f(x)\) on the interval \([a,b]\) by using the three points \((a,f(a))\), \((m,f(m))\), and \((b,f(b))\) where \(m=\frac{a+b}{2}\) is the midpoint of the two boundary points.
We want to find constants \(A_1\), \(A_2\), and \(A_3\) such that the integral \(\int_a^b f(x) dx\) can be written as a linear combination of \(f(a)\), \(f(m)\), and \(f(b)\). Specifically, we want to find constants \(A_1\), \(A_2\), and \(A_3\) in terms of \(a\), \(b\), \(f(a)\), \(f(b)\), and \(f(m)\) such that \[\begin{equation} \int_a^b f(x) dx = A_1 f(a) + A_2 f(m) + A_3 f(b) \end{equation}\] is exact for all constant, linear, and quadratic functions. This would guarantee that we have an exact integration method for all polynomials of order 2 or less but should serve as a decent approximation if the function is not quadratic.
Exercise 4.35 Draw a picture showing what the previous two paragraphs discussed.
Exercise 4.36 Follow these steps to find \(A_1\), \(A_2\), and \(A_3\).
Verify that \[\begin{equation} \int_a^b 1 dx = b-a = A_1 + A_2 + A_3. \end{equation}\]
Verify that \[\begin{equation} \int_a^b x dx = \frac{b^2 - a^2}{2} = A_1 a + A_2 \left( \frac{a+b}{2} \right) + A_3 b. \end{equation}\]
Verify that \[\begin{equation} \int_a^b x^2 dx = \frac{b^3 - a^3}{3} = A_1 a^2 + A_2 \left( \frac{a+b}{2} \right)^2 + A_3 b^2. \end{equation}\]
Verify that the above linear system of equations has the solution \[\begin{equation} A_1 = \frac{b-a}{6}, \quad A_2 = \frac{4(b-a)}{6}, \quad \text{and} \quad A_3 = \frac{b-a}{6}. \end{equation}\]
Exercise 4.37 At this point we can see that an integral can be approximated as \[\begin{equation} \int_a^b f(x) dx \approx \left( \frac{b-a}{6} \right) \left( f(a) + 4f\left( \frac{a+b}{2} \right) + f(b) \right) \end{equation}\] and the technique will give an exact answer for any polynomial of order 2 or below.
Verify the previous sentence by integrating \(f(x) = 1\), \(f(x) = x\) and \(f(x) = x^2\) by hand on the interval \([0,1]\) and using the approximation formula \[\begin{equation} \int_a^b f(x) dx \approx \left( \frac{b-a}{6} \right) \left( f(a) + 4f\left( \frac{a+b}{2} \right) + f(b) \right). \end{equation}\]
Use the method described above to approximate the area under the curve \(f(x) = (1/5) x^2 (5-x)\) on the interval \([1,4]\). To be clear, you will be using the points \(a=1, m=2.5\), and \(b=4\) in the above derivation.
Next find the exact area under the curve \(f(x) = (1/5) x^2 (5-x)\) on the interval \([1,4]\).
What do you notice about the two areas? What does this sample exercise tell you about the formula that we derived above?
To make the punchline of the previous exercises a bit more clear, using the formula \[\begin{equation} \int_a^b f(x) dx \approx \left( \frac{b-a}{6} \right) \left( f(a) + 4 f(m) + f(b) \right) \end{equation}\] is the same as fitting a parabola to the three points \((a,f(a))\), \((m,f(m))\), and \((b,f(b))\) and finding the area under the parabola exactly. That is exactly the step up from the trapezoid rule and Riemann sums that we were after:
Riemann sums approximate the function with constant functions,
the trapezoid rule uses linear functions, and
now we have a method for approximating with parabolas.
To improve upon this idea we now examine the problem of partitioning the interval \([a,b]\) into small pieces and running this process on each piece. This is called Simpson’s Rule for integration.
Definition 4.4 (Simpson’s Rule) Now we put the process explained above into a form that can be coded to approximate integrals. We call this method Simpson’s Rule after Thomas Simpson (1710-1761) who, by the way, was a basket weaver in his day job so he could pay the bills and keep doing math.
First partition \([a,b]\) into the set \(\{x_0=a, x_1, x_2, \ldots, x_{n-1}, x_n=b\}\).
On each part of the partition approximate the area with a parabola: \[\begin{equation} A_j = \frac{1}{6} \left[ f(x_j) + 4 f\left( \frac{x_j+x_{j-1}}{2} \right) + f(x_{j-1}) \right]\left( x_j - x_{j-1} \right). \end{equation}\]
Approximate the integral as \[\begin{equation} \int_a^b f(x) dx = \sum_{j=1}^n A_j. \end{equation}\]
Exercise 4.38 Write a Python function that implements Simpson’s Rule. You should ALWAYS start by writing pseudo-code as comments in your file. You should not need a loop in your function.
Exercise 4.39 Test your function on known integrals and approximate the order of the error based on the mesh size.
Exercise 4.40 We have spent a lot of time over the past many pages building approximations of the order of the error for numerical integration and differentiation schemes. It is now up to you. Build a numerical experiment that allows you to conjecture the order of the approximation error for Simpson’s rule. Remember that the goal is to answer the question:
If I approximate the integral with a fixed \(\Delta x\) and find an absolute error of \(P\), then what will the absolute error be using a width of \(\Delta x / M\)?
Thus far we have three numerical approximations for definite integrals: Riemann sums (with rectangles), the trapezoidal rule, and Simpsons’s rule. There are MANY other approximations for integrals and we leave the further research to the curious reader.
Theorem 4.2 (Numerical Integration Schemes) Let \(f(x)\) be a continuous function on the interval \([a,b]\). The integral \(\int_a^b f(x) dx\) can be approximated with any of the following. \[\begin{equation} \begin{aligned} &\text{Riemann Sum: } \int_a^b f(x) dx \approx \sum_{j=1}^N f(x_j) \Delta x \\ & \qquad \text{Error for Left and Right Riemann Sums: } \mathcal{O}(\Delta x) \\ & \qquad \text{Error for Midpoint Riemann Sums: } \mathcal{O}(\Delta x^2) \\ &\text{Trapezoidal Rule: } \int_a^b f(x) dx \approx \frac{1}{2} \sum_{j=1}^N \left( f(x_j) + f(x_{j-1}) \right) \Delta x \\ & \qquad \text{Error for Trapezoidal Rule: } \mathcal{O}(\Delta x^2) \\ &\text{Simpson's Rule: } \int_a^b f(x) dx \approx \frac{1}{6} \sum_{j=1}^N \left( f(x_j) + 4 f\left( \frac{x_j + x_{j-1}}{2} \right) + f(x_{j-1}) \right) \Delta x \\ & \qquad \text{Error for Simpson's Rule: } \mathcal{O}(\Delta x^4) \\ \end{aligned} \end{equation}\] where \(\Delta x = x_j - x_{j-1}\) and \(N\) is the number of subintervals.
Exercise 4.41 Theorem 4.2 simply states the error rates for our three primary integration schemes. For this exercise you need to empirically verify these error rates. Use the integration problem and exact answer \[\begin{equation} \int_0^{\pi/4} e^{3x} \sin(2x) dx = \frac{3}{13} e^{3\pi/4} + \frac{2}{13} \end{equation}\] and write code that produces a log-log error plot with \(\Delta x\) on the horizontal axis and the absolute error on the vertical axis. Fully explain how the error rates show themselves in your plot.
4.3.4 Integration with numpy and scipy
In numpy there is a nice tool called np.trapz() that implements the trapezoidal rule. In the following exercise you will find several examples of the np.trapz() command. Use these examples to determine how the command works to integrate functions.
Exercise 4.42 First we will approximate the integral \(\int_{-2}^2 x^2 dx\). The exact answer is \[\begin{equation} \int_{-2}^2 x^2 dx = \frac{x^3}{3} \Big|_{-2}^2 = \frac{16}{3} = 5.3333\dots. \end{equation}\]
import numpy as np
x = np.linspace(-2,2,100)
dx = x[1]-x[0]
y = x**2
print("Approximate integral is ",np.trapz(y)*dx)Next we will approximate \(\int_0^{2\pi} \sin(x) dx\). We know that the exact value is 0.
import numpy as np
x = np.linspace(0,2*np.pi,100)
dx = x[1]-x[0]
y = np.sin(x)
print("Approximate integral is ",np.trapz(y)*dx)Pick a function and an interval for which you know the exact definite integral. Demonstrate how to use np.trapz() on your definite integral.
Exercise 4.43 Notice in the last examples that we multiplied the result of the np.trapz() command by dx. Why did we do this? What is the np.trapz() command doing without the dx?
In the scipy library there is a more general tool called scipy.integrate.quad(). The term “quad” is short for “quadrature.” In numerical analysis literature rules like Simpson’s rule are called quadrature rules for integration. The function scipy.integrate.quad() accepts a Python function (or a lambda function) and the bounds of the definite integral. It outputs an approximation of the integral along with an approximation of the error in the integral calculation. See the Python code below.
import numpy as np
import scipy.integrate
f = lambda x: x**2
I = scipy.integrate.quad(f,-2,2)
print(I)Exercise 4.44 What are the advantages and disadvantages to using the scipy.integrate.quad() command as compared to the np.trapz() command.
Exercise 4.45 If you have data for the hourly rate at which water is being drained from a dam and you want to find the total amount of water drained over the course of the time in the dataset, then which of the tools that we know would you use? Why?
4.4 Algorithm Summaries
Exercise 4.46 Starting from Taylor series prove that \[\begin{equation} f'(x) \approx \frac{f(x+h) - f(x)}{h} \end{equation}\] is a first-order approximation of the first derivative of \(f(x)\). Clearly describe what “first-order approximation” means in this context.
Exercise 4.47 Starting from Taylor series prove that \[\begin{equation} f'(x) \approx \frac{f(x+h) - f(x-h)}{2h} \end{equation}\] is a second-order approximation of the first derivative of \(f(x)\). Clearly describe what “second-order approximation” means in this context.
Exercise 4.48 Starting from Taylor series prove that \[\begin{equation} f''(x) \approx \frac{f(x+h) - 2f(x) + f(x-h)}{h^2} \end{equation}\] is a second-order approximation of the second derivative of \(f(x)\). Clearly describe what “second-order approximation” means in this context.
Exercise 4.49 Explain how to approximate the value of a definite integral with Riemann sums. When will the Riemann sum approximation be exact? The Riemann sum approximation is first order. Explain what “first order” means for calculating a definite integral.
Exercise 4.50 Explain how to approximate the value of a definite integral with the Trapezoid rule. When will the Trapezoid rule approximation be exact? The Trapezoidal rule approximation is second order. Explain what “second order” means for calculating a definite integral.
Exercise 4.51 Explain how to approximate the value of a definite integral with Simpson’s rule. Give the full mathematical details for where Simpson’s rule comes from. When will the Simpson’s rule approximation be exact? The Simpson’s rule approximation is fourth order. Explain what “fourth order” means for calculating a definite integral.
4.5 Problems
Exercise 4.52 For each of the following numerical differentiation formulas
- prove that the formula is true and
- find the order of the method.
To prove that each of the formulas is true you will need to write the Taylor series for all of the terms in the numerator on the right and then simplify to solve for the necessary derivative. The highest power of the remainder should reveal the order of the method.
\(f'(x) \approx \frac{\frac{1}{12} f(x-2h) - \frac{2}{3} f(x-h) + \frac{2}{3} f(x+h) - \frac{1}{12} f(x+2h)}{h}\)
\(f'(x) \approx \frac{-\frac{3}{2} f(x) + 2 f(x+h) - \frac{1}{2} f(x+2h)}{h}\)
\(f''(x) \approx \frac{-\frac{1}{12} f(x-2h) + \frac{4}{3} f(x-h) - \frac{5}{2} f(x) + \frac{4}{3} f(x+h) - \frac{1}{12} f(x+2h)}{h^2}\)
\(f'''(x) \approx \frac{-\frac{1}{2} f(x-2h) + f(x-h) - f(x+h) + \frac{1}{2} f(x+2h)}{h^3}\)
Exercise 4.53 Write a function that accepts a list of \((x,y)\) ordered pairs from a spreadsheet and returns a list of \((x,y)\) ordered pairs for a first order approximation of the first derivative of the underlying function. Create a test spreadsheet file and a test script that have graphical output showing that your function is finding the correct derivative.
Exercise 4.54 Write a function that accepts a list of \((x,y)\) ordered pairs from a spreadsheet or a *.csv file and returns a list of \((x,y)\) ordered pairs for a second order approximation of the second derivative of the underlying function. Create a test spreadsheet file and a test script that have graphical output showing that your function is finding the correct derivative.
Exercise 4.55 Write a function that implements the trapezoidal rule on a list of \((x,y)\) order pairs representing the integrand function. The list of ordered pairs should be read from a spreadsheet file. Create a test spreadsheet file and a test script showing that your function is finding the correct integral.
Exercise 4.56 Use numerical integration to answer the question in each of the following scenarios
- We measure the rate at which water is flowing out of a reservoir (in gallons per second) several times over the course of one hour. Estimate the total amount of water which left the reservoir during that hour.
| time (min) | 0 | 7 | 19 | 25 | 38 | 47 | 55 |
|---|---|---|---|---|---|---|---|
| flow rate (gal/sec) | 316 | 309 | 296 | 298 | 305 | 314 | 322 |
You can download the data directly from the github repository for this course with the code below.
import numpy as np
import pandas as pd
data = np.array(pd.read_csv('https://github.com/gustavdelius/NumericalAnalysis2024/raw/main/data/Calculus/waterflow.csv'))- The department of transportation finds that the rate at which cars cross a bridge can be approximated by the function \[\begin{equation} f(t) = \frac{22.8 }{3.5 + 7(t-1.25)^4} , \end{equation}\] where \(t=0\) at 4pm, and is measured in hours, and \(f(t)\) is measured in cars per minute. Estimate the total number of cars that cross the bridge between 4 and 6pm. Make sure that your estimate has an error less than 5% and provide sufficient mathematical evidence of your error estimate.
Exercise 4.57 Consider the integrals \[\begin{equation}
\int_{-2}^2 e^{-x^2/2} dx \quad \text{and} \quad \int_0^1 \cos(x^2) dx.
\end{equation}\] Neither of these integrals have closed-form solutions so a numerical method is necessary. Create a log-log plot that shows the errors for the integrals with different values of \(h\) (log of \(h\) on the \(x\)-axis and log of the absolute error on the \(y\)-axis). Write a complete interpretation of the log-log plot. To get the exact answer for these plots use Python’s scipy.integrate.quad command. (What we are really doing here is comparing our algorithms to Python’s scipy.integrate.quad() algorithm).
Exercise 4.58 Go to data.gov or the World Health Organization Data Repository and find data sets for the following tasks.
Find a data set where the variables naturally lead to a meaningful derivative. Use appropriate code to evaluate and plot the derivative. If your data appears to be subject to significant noise then you may want to smooth the data first before doing the derivative. Write a few sentences explaining what the derivative means in the context of the data.
Find a data set where the variables naturally lead to a meaningful definite integral. Use appropriate code to evaluate the definite integral. If your data appears to be subject to significant noise then you might want to smooth the data first before doing the integral. Write a few sentences explaining what the integral means in the context of the data.
In both of these tasks be very cautious of the units on the data sets and the units of your answer.
Exercise 4.59 Numerically integrate each of the functions over the interval \([-1,2]\) with an appropriate technique and verify mathematically that your numerical integral is correct to 10 decimal places. Then provide a plot of the function along with its numerical first derivative.
\(f(x) = \frac{x}{1+x^4}\)
\(g(x) = (x-1)^3 (x-2)^2\)
\(h(x) = \sin\left(x^2\right)\)
Exercise 4.60 A bicyclist completes a race course in 90 seconds. The speed of the biker at each 10-second interval is determined using a radar gun and is given in the table in feet per second. How long is the race course?
| Time (sec) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
|---|---|---|---|---|---|---|---|---|---|---|
| Speed (ft/sec) | 34 | 32 | 29 | 33 | 37 | 40 | 41 | 36 | 38 | 39 |
You can download the data with the following code.
import numpy as np
import pandas as pd
data = np.array(pd.read_csv('https://github.com/gustavdelius/NumericalAnalysis2024/raw/main/data/Calculus/bikespeed.csv'))4.6 Projects
In this section we propose several ideas for projects related to numerical Calculus. These projects are meant to be open ended, to encourage creative mathematics, to push your coding skills, and to require you to write and communicate your mathematics.
4.6.1 Galaxy Integration
To analyse the light from stars and galaxies, scientists use a spectral grating (fancy prism) to split it up into the different frequencies (colours). We can then measure the intensity (brightness) of the light (in units of Watts per square meter) at each frequency (measured in Hertz), to get intensity per frequency (Watts per square meter per Hertz, W/(m\(^2\) Hz)). Light from the dense opaque surface of a star produces a smooth rainbow, which produces a continuous curve when we plot intensity versus frequency. However, stars are also surrounded by thin gas which either emits or absorbs light at only a specific set of frequencies, called spectral lines. Every chemical element produces a specific set of lines (or peaks) at fixed frequencies, so by identifying the lines, we can tell what types of atoms and molecules a star is made of. If the gas is cool, then it will absorb light at these wavelengths, and if the gas is hot then it will emit light at these wavelengths. For galaxies, on the other hand, we expect mostly emission spectra: light emitted from the galaxy.
For this project we will be analysing the galaxy “ngc 1275.” The black hole at the centre of this galaxy is often referred to as the “Galactic Spaghetti Monster” since the magnetic field “sustains a mammoth network of spaghetti-like gas filaments around it.” You can download the data file associated with this project with the following Python code.
import numpy as np
import pandas as pd
ngc1275 = np.array(pd.read_csv('https://github.com/gustavdelius/NumericalAnalysis2024/raw/main/data/Calculus/ngc1275.csv'))In the data you will see the spectral data measuring the light intensity from ncg 1275 at several different wavelengths (measured in Angstroms ). You will notice in this data set that there are several emission lines at various wavelengths. Of particular interest are the peaks near \(3800\) Angstroms, \(5100\) Angstroms, \(6400\) Angstroms, and the two peaks around \(6700\) Angstroms. The data set contains 1,727 data points at different wavelengths. Your first job will be to transform the wavelength data to frequency via the formula \[\begin{equation} \lambda = \frac{c}{f}, \end{equation}\] where \(\lambda\) is the wavelength, \(c\) is the speed of light, and \(f\) is the frequency (measured in Hertz). Be sure to double check the units. Given the inverse relationship between frequency and wavelength you should see the emission lines flip to the other side of the plot (right-to-left or left-to-right).
The strength of each emission line (in W/m\(^2\)) is defined as the relative intensity of each peak across the associated frequencies. Note that you are not interested in the intensity of the continuous spectrum – just the peaks. That is to say that you are only interested in the area above the background curve and the background noise.
Your primary task is to develop a process for analysing data sets like this so as to determine the strength of each emission lines. You must demonstrate your process on this particular data set, but your process must be generalizable to any similar data set. Your process must clearly determine the strength of peaks in data sets like this and you must apply your procedure to determine the strength of each of these four lines with an associated margin of error. Keep in mind that you will first want to first develop a method for removing the background noise. Finally, the double peak near \(6700\) Angstroms needs to be handled with care: the strength of each emission line is only the integral over one peak, not two, so you will need to determine a way to separate these peaks.
Finally, it would be cool, but is not necessary, to report on which chemicals correspond to the emission lines in the data. Remember that the galaxy is far away and hence there is a non-trivial red-shift to consider. This will take some research but if done properly will likely give a lot more merit to your paper.
4.6.2 Higher Order Integration
Riemann sums can be used to approximate integrals and they do so by using piecewise constant functions to approximate the function. The trapezoidal rule uses piece wise linear functions to approximate the function and then the area of a trapezoid to approximate the area. We saw earlier that Simpson’s rule uses piece wise parabolas to approximate the function. The process which we used to build Simpson’s rule can be extended to any higher-order polynomial. Your job in this project is to build integration algorithms that use piece wise cubic functions, quartic functions, etc. For each you need to show all of the mathematics necessary to derive the algorithm, provide several test cases to show that the algorithm works, and produce a numerical experiment that shows the order of accuracy of the algorithm.
4.6.3 Dam Integration
Go to the USGS water data repository:
https://maps.waterdata.usgs.gov/mapper/index.html.
Here you will find a map with information about water resources around the country.
Zoom in to a dam of your choice (make sure that it is a dam).
Click on the map tag then click “Access Data”
From the drop down menu at the top select either “Daily Data” or “Current / Historical Data.” If these options do not appear then choose a different dam.
Change the dates so you have the past year’s worth of information.
Select “Tab-separated” under “Output format” and press Go. Be sure that the data you got has a flow rate (ft\(^3\)/sec).
At this point you should have access to the entire data set. Copy it into a
csvfile and save it to your computer.
For the data that you just downloaded you have three tasks: (1) plot the data in a reasonable way giving appropriate units, (2) find the total amount of water that has been discharged from the dam during the past calendar year, and (3) report any margin of error in your calculation based on the numerical method that you used in part (2).